Hacking the Wiki Game
The Wiki Game is a hypertextual game designed to work specifically with Wikipedia. The Wiki Game (or Wikirace, Wikispeedia, WikiLadders) requires only a computer, access to Wikipedia and a web browser to play. The objective is to reach a given home article in the smallest number of clicks, starting from the Random page link of Wikipedia.
Its origin is unclear, but one of the first occurences on the web dates as far back as 2008.[1] Many variations exist, but arguably the most famous one is Six Degrees to Hitler, where the objective is to reach the article of Adolf Hitler. The name is a play on the Six Degrees of Separation theory (stating that everyone on Earth is six or fewer steps away, by way of introduction, from any other person in the world).
Our goal was to analyse this game by studying the network of Wikipedia pages and links between them, using tools such as Python, Gephi, SNAP. As the English Wikipedia database contains 36,615,821 pages with 4,905,818 articles,[2] analysis is very slow. We chose to study the Simple English Wikipedia network instead.[3]
Contents
Simple English Wiki network: birds-eye view
Wikipedia as a scale-free network
The Wikipedia network contains many special pages. Therefore, pages are given a namespace; a namespace equal to 0 signifies an article. Links between pages exist in two forms: regular links appear as blue, while a link to a nonexistent page appears as red. Often, a link redirects a page to another page. Removing all redirects, and retaining only the articles and links between them significantly reduces the data size (see the infobox). The resulting network of 113,202 nodes and 4,525,556 links was the starting point of our analyses.
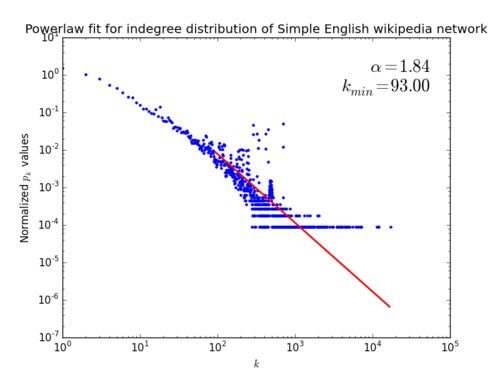
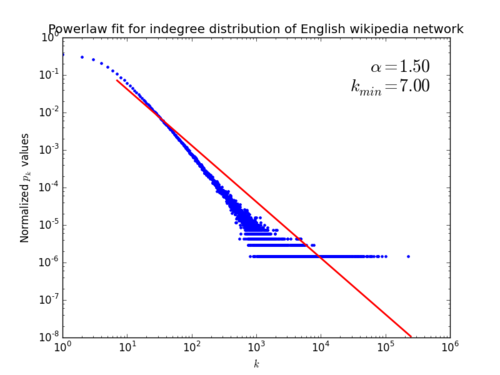
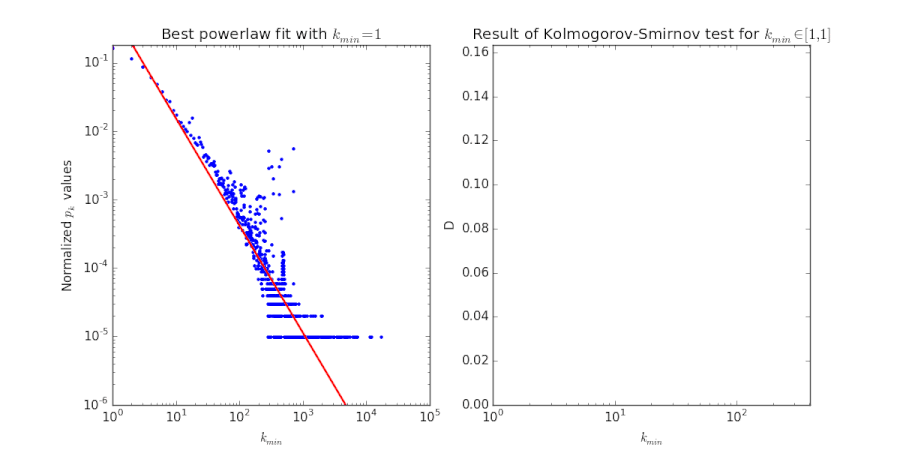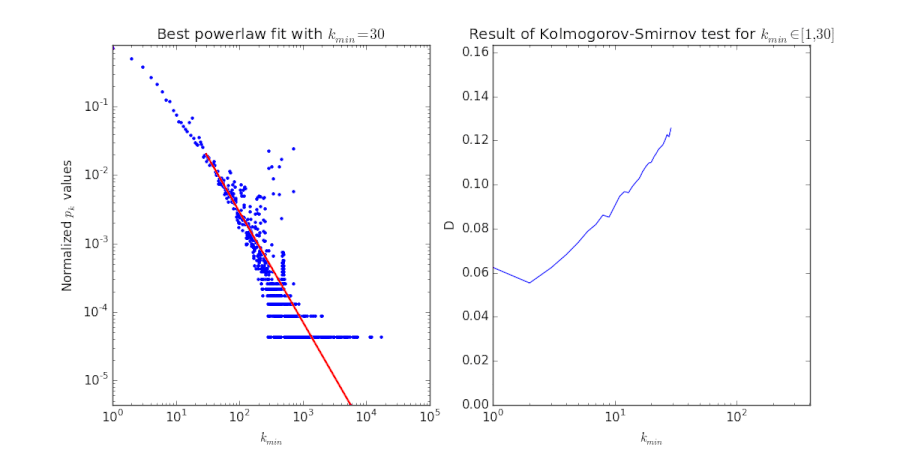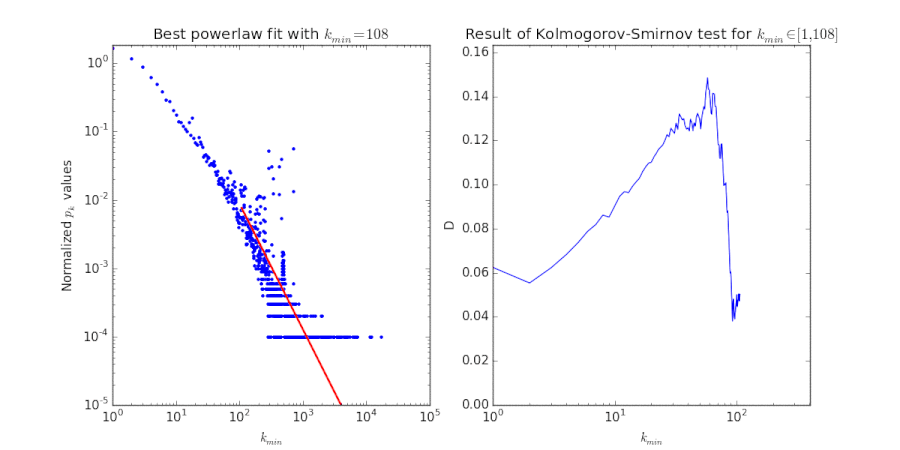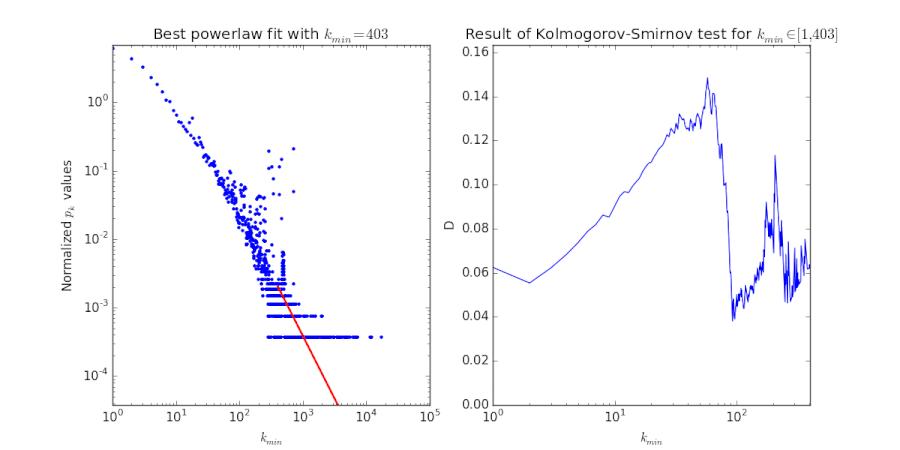
As scale-free networks are known to be prone to attacks,[4] and our goal is to attack the network as to disrupt the Wiki Game, our first goal was to study the scale-free property. The indegree distribution of the Simple English wiki and a polynomial fit (found using powerlaw) is shown on the left; the indegree distribution of the English wiki network of 2007 is shown on the right. The apparent outliers in the left graph can be explained by the existence of very poorly connected cliques of large degree (e.g. Ablon is part of a degree-704 clique).
The right fit is very nice: it immediately shows the scale-free property in the Wikipedia network. The left fit is somewhat unsatisfactory; is somewhat high and the fit is not very close. This urged us to look at the inner workings of this fitting procedure.[4] It works by considering all possible values for , computing the best powerlaw fit for this specific value. It then chooses the value
This procedure is called the Kolmogorov-Smirnov test. A visualisation of this procedure is given in the figure below. We see that while this value for yields a slightly unfortunate result, there is no for which the goodness of fit is close. Of course, this fit can be made much better by excluding the outliers.
We conclude that both the English and the Simple English Wikipedia network are scale-free. Both exponents are smaller than 2, which is impossible for , because the average degree diverges with system size. Apparently our networks aren't large enough to exhibit this: the largest indegree is 17222 and 101110,[5] respectively.
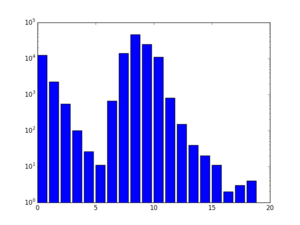
Wikipedia diameter
As we can fairly quickly determine the path length distribution for any node in the network, we can also look at the distribution of the longest shortest path to any target node. The figure on the right shows the longest shortest path distribution. We can see two clear spikes, one centered around zero, and one centered around 8. Pages belonging to the mass centered around zero are pages that are very poorly connected, so while the longest path to get to such a page is very low, the number of pages that can reach such a page is also very low.
The Simple English Wikipedia shows a diameter of 18; the English Wikipedia has at least 77; this is due to long chains of articles.[6]
Disrupting the wiki game
As a mathematical problem, we can restate the Wiki Game as follows. Given a network , a target and a source , we opt to find a shortest path of length from to . As the source is a random element from , one interesting measure is the shortest path length distribution
With this, we can look at average shortest path length
and the variance
Of course, our goal is to disrupt the Wiki Game as efficiently as possible. The probability of starting the game from a page must equal ; this means that we want to find pages or pagelinks which, if deleted, increase the average path length the most. The size of our network forces us to find a smart attack strategy rather than simply trying each page or link. Effectivity of an attack algorithm on a page is measured by the number of pages/links that it removes before increasing by 0.5. We define this as the page robustness with respect to this attack.
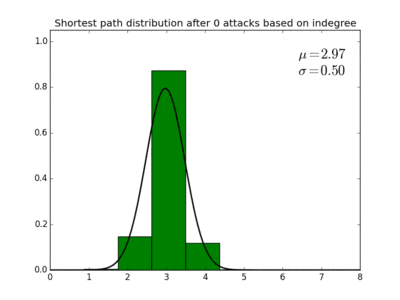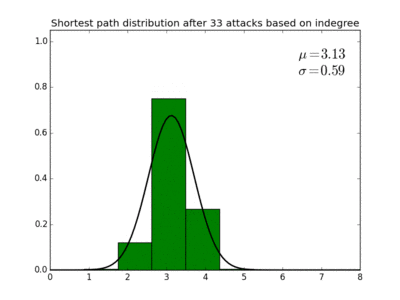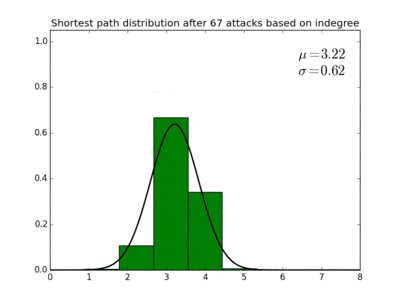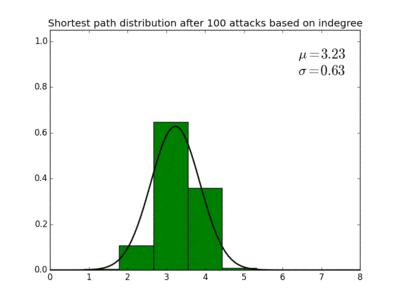
Taking a highest indegree attack strategy as an example, we can calculate with target node Hitler as it is being attacked. This yields the figure to the right. We see that this distribution is more or less binomial.
Relative betweenness
We define the relative betweenness of a node or edge as the number of shortest paths to target node that pass through the node or edge[7]. In order to find the relative betweenness of a node or edge, we define the following variables and sets:
- The set as the set of predecessors of with ;
- The set as the set of successors of such that ;
- The geodesic weight (with );
- The relative betweenness of an edge: ;
- The relative betweenness of a node: .
Relative betweenness attack strategy
- Do a breadth-first search to get geodesic lengths for every node.
- Calculate the weight for every node
- Calculate the average geodesic length
- While average geodesic length has not increased with at least 0.5:
- For all nodes in reverse order of geodesic length:
- Calculate relative edge betweenness of all edges with
- Calculate relative node betweenness of
- Remove node or edge with highest betweenness
- Update geodesic lengths and node weights for affected nodes
- For all nodes in reverse order of geodesic length:
Attacking nodes
Node attacks were done using the following strategies:
- Highest indegree
- with highest indegree; executing one attack takes milliseconds, as we only have to loop over the predecessors of .
- Highest relative betweenness
- with highest ; takes a few seconds, as we have to traverse all nodes that can reach .
We quickly realized that while of theoretical relevance, attacking nodes would never work in practice as it requires removing entire Wikipedia pages. Therefore we moved on to the more realistic edge attack strategies.
Attacking edges
We execute attacks on edges using the following metrics:
- Highest indegree
- Choose the with highest indegree and remove .
- Highest relative node betweenness
- Edge on shortest path coming from node with highest relative node betweenness; we select the node with highest relative betweenness, and pick with highest node betweenness.
- Highest relative edge betweenness
- This is self-explanatory.
- Greedy
- loops over all nodes and chooses the edge which removal increases the average path length the most.
The definition of relative betweenness implies that for it holds that , so that the second and third algorithm attack the same edge in all cases.
Numerical results
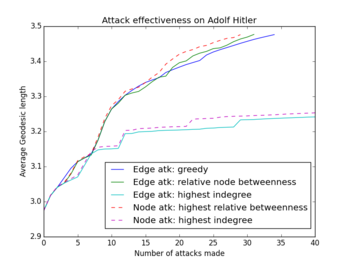
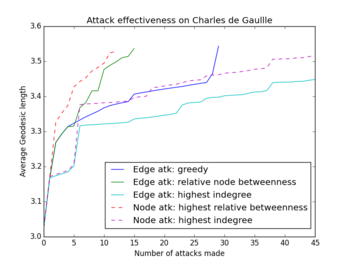
The size of the network made it impossible to test our attack strategies on all pages. Moreover, the majority of pages is hardly robust at all. We ultimately chose the 48 Time People of the Year as test subjects; this list includes Mahatma Gandhi, our beloved Adolf, Queen Elizabeth II, and Mark Zuckerberg. These 48 pages are all relatively well-connected with indegrees ranging from 14 to 649, and average geodesic lengths ranging from 2.83 to 3.65.
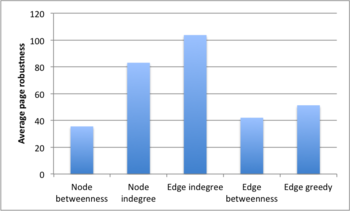
Looking at the first figure below, we see that (relative) betweenness is the attack strategy producing the lowest average robustness. Moreover, attacks based on indegree perform badly.
Before simulating, we conjectured that the greedy algorithm would find optimal results, seeing it attacks the locally optimal edge. Looking at the middle figure, this conjecture is approximately correct. In the right figure however, we see that the greedy and betweenness strategy (blue resp. green line in the graph) attack the same edge in iterations 1 to 4. We also see that the green line stalls at iteration 4 to surge again from iteration 5 onward. Apparently, choosing the local optimum in iteration 4 does not imply a global optimum.
The Wiki Game in practice
After working with all this data, we decided it would be fun to test out how feasible an actual Wiki attack was. Of course, node attacks imply removing a Wikipedia page which is completely undoable. Removing edges however is easily done.
Removing links from articles was spotted and reverted quickly (see Figure to the left) so we decided to rewrite the sentences containing the links instead.
Attacking Justin Bieber
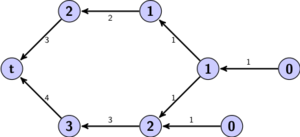
Nobody actually likes Justin Bieber[citation needed] and as such he was an obvious target. Fortunately his page is somewhat poorly connected, with only 14 links pointing to his article. His relative betweenness robustness was found to be just two by removing
| # of edges removed | |
|---|---|
| 0 | 3.8563 |
| 1 | 4.0103 |
| 2 | 4.5282 |
As was to be expected, Justin Bieber is a very easy target; we needed just 2 links to increase his average path length with a half.
Eurozone? όχι!
While everybody is voting for or against #GREXIT, we decided to take a stand on this issue by removing not Greece from the Eurozone but the Eurozone from Wikipedia. Our relative betweenness attack strategy yielded a robustness of 7, with
- (European Union, Eurozone)
- (ISO 4217, Eurozone)
- (Bulgaria, Eurozone)
- (Montenegro, Eurozone)
- (Euro, Eurozone)
- (1999, Eurozone)
- (2010, Eurozone)
The Euro page has 6 explicit mentions of Eurozone, so we opted to remove (2015, Eurozone) instead.
| # of edges removed | |
|---|---|
| 0 | 3.2545 |
| 1 | 3.2848 |
| 2 | 3.3751 |
| 3 | 3.4691 |
| 4 | 3.5611 |
| 5 | 3.6191 |
| 6 | 3.6670 |
| 7 | 3.7359 |
| 8[9] | 3.9015 |
We see that as The Eurozone article is reasonably well connected, we have to remove 7 links to increase its average path length by a half.
Mending the Wiki Game: putting Britney back in the spotlight
Rather than removing links to make a page less visible, we can also add links to improve the visibility of a page. This is a very different problem, as edge not yet existing in the network could be added. So the goal was to both find links that would be reasonable to add, and find a fast heuristic to find links the would provide a good improvement on the average geodesic length.
We decided to see if we could improve the average geodesic length of famous singer Britney Spears. To this end we selected various nodes which themselves have a very low average geodesic length, and where a link to Britney could be added. United States and Americans seemed the best candidates.
| Links added from | |
|---|---|
| 3.4018 | |
| United States | 2.9342 |
| United States, Americans | 2.8943 |
Adding links to Britney Spears to these pages reduced the average geodesic length by more than 0.5. An important advantage of adding links, rather than removing them, is that it is not considered vandalism if the information is correct. This last note makes algorithmic selection of pages more challenging, as most pairs of pages are not directly related, making it hard to add relevant information about that page. For example, it would be harder to add content that would link Britney Spears to Germany.
Attacking the wiki network with ulterior motives
We have seen that editing a Wikipedia page is possible, and will have a real effect on the average geodesic length of the page. While these examples are purely for academic purposes, it is very possible an editor can have an ulterior motive behind making an edit. A good example of such an edit would be for a person to add links in Wikipedia to their own page as a form of PR.
As it turns out, Conflict of interest editing happens a lot on Wikipedia. There are many known cases[10][11] where large companies and political parties have made edits to Wikipedia pages to either improve their own brand or to try to deface the pages of their competitors.
A big difference between the edits made by these parties and our strategy is that they are often aimed at modifying the content of a page, while we modifying the link connectivity of a page. Often these edits are very childish and are quickly reverted; see figure.
Final thoughts
Even though our research mentions Wikipedia, we did most of the analysis on the Simple English Wiki. We did not have the hardware available to import and process recent data of Wikipedia and run our algorithms. With a computationally stronger system and optimized algorithms, this would be more feasible.
The focus of this research was mainly on disrupting the Wiki Game by edge removal. Investigating algorithms for edge addition was not inside the scope of this research, as removing links from Wikipedia pages is easier to achieve than strategically adding links to pages (as this would require that the links are relevant). With more information, however, it would be possible to develop an algorithm that suggests pages of the same category, or that suggests to link to pages that already link to the target page.
References
- ↑ http://www.nintendoworldreport.com/forums/index.php?topic=26255.0
- ↑ https://en.wikipedia.org/wiki/Wikipedia:Statistics
- ↑ https://dumps.wikimedia.org/simplewiki/latest/
- ↑ 4.0 4.1 Barabási, Albert-László, Network Science, 2015.
- ↑ We were unable to determine with 100% accuracy which page this is as the network data was anonymized; we suspect however that it is United States
- ↑ http://mu.netsoc.ie/wiki/
- ↑ http://www.sciencedirect.com/science/article/pii/S0378873307000731#
- ↑ https://simple.wikipedia.org/w/index.php?title=Angela_Merkel&type=revision&diff=5163294&oldid=5163092
- ↑ Not actually performed.
- ↑ https://en.wikipedia.org/wiki/Conflict-of-interest_editing_on_Wikipedia#Incidents
- ↑ http://www.bbc.com/news/technology-28481876















![{\displaystyle \operatorname {Var} (N(t))={\frac {1}{|V|}}\sum _{p\in \mathbb {N} }N(t,p)[p-{\overline {N}}(t)]^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ede541868c53ebeb34320c012dcdef11fd6178ca)